Discrete and continuous models for tissue growth and shrinkage

In this post Dr. Christian Yates summarises his recent paper “Discrete and continuous models for tissue growth and shrinkage”, on modelling tissue growth and shrinkage using mathematical models that explicitly incorporate randomness in the tissue deformation process.

The mathematical theme which underlies my research is the development of methodologies for modelling complex biological systems in which randomness (often referred to as stochasticity) plays an important role. In particular, I am interested in modelling complex processes in which the incorporation of noise can produce mean behaviour that differs significantly from the behaviour of a corresponding deterministic model.  I am also interested in modelling systems for which, because of their inherent dependence on noise, there is no deterministic counterpart.

The incorporation of domain growth into stochastic models of biological processes is of increasing interest to mathematical modellers and biologists alike. In many situations, especially in developmental biology, the growth of the underlying tissue domain plays an important role in the redistribution of particles (be they cells or molecules) which may move and react atop the domain. Although such processes have largely been modelled using deterministic (non-random), continuum models, there is an increasing appetite for individual-based stochastic (random) models, which can capture the fine detail of the biological movement processes that are being elucidated by modern experimental techniques, and can also incorporate the inherent stochasticity of such systems.

I recently had a paper published in the Journal of Theoretical Biology on this subject. In this paper I study a simple stochastic model of domain growth/shrinkage. From a basic version of this model, Hywood et al. were able to derive a Fokker-Plank equation (FPE) (in this case, an advection-diffusion partial differential equation on a growing domain), which describes the evolution of the probability density of some tracer particles on the domain. My paper extends their work so that a variety of different domain growth mechanisms can be incorporated. I demonstrate a good agreement between the mean tracer density and the solution of the FPE in each case. In addition I incorporate domain shrinkage (via element death) into my individual-level model and demonstrate that I am also able to derive coefficients for the FPE in this case. For situations in which the drift and diffusion coefficients are not readily available, I introduce a numerical coefficient estimation approach.

The basic individual-based model I use to represent tissue growth/shrinkage is a one-dimensional domain of made up initially of contiguous elements each of length Δ. I incorporate growth and shrinkage into this individual-level model by allowing these elements to undergo ‘proliferation events’ and ‘death events’, which are analogous to biological cell division and cell death. In order to better understand the dynamics of the domain growth/shrinkage process, we can place tracer particles on top of a subset of the domain elements. We say that these domain elements are ‘marked’. The movement of the domain elements and the tracer particles resulting from a growth or death event are summarised in Figures 1 and 2.

(a)

(b)

Figure 1: Examples of growth and division events. Domain elements are white boxes and tracer particles are represented by smaller red boxes atop particular ‘marked’ elements. In each subfigure the top configuration shows a domain before a growth event and the bottom a domain configuration after a growth event. (a) An unmarked element is chosen to divide. It does so by pushing itself and the intervals to its right one element length, Δ. Tracer particles move with the elements and a new element (hatched) is inserted in the empty space. (b) A marked element is selected to divide. It undergoes the same movement procedure as for the unmarked element taking its tracer particle with it. Again a new element (hatched) is inserted in the vacant space.

(a)

(b)

(c)

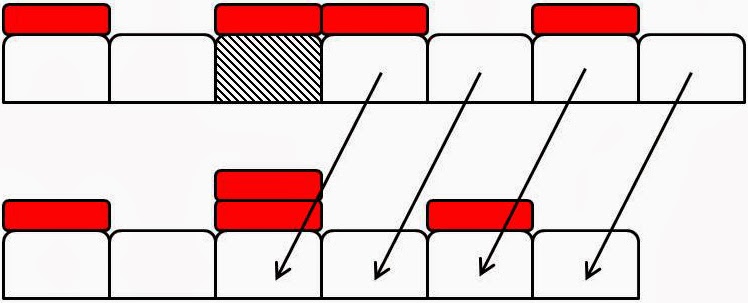
Figure 2: Examples of element death events. Domain elements are white boxes and tracer particles are represented by smaller red boxes atop particular ‘marked’ elements. In each subfigure the top configuration shows a domain before a death event and the bottom a domain configuration after a death event. (a) An unmarked element (hatched) is chosen to die. It is removed from the domain and intervals to its right move leftwards by one element length, Δ, to fill the space. Tracer particles move with their elements. (b) A marked element (hatched) is chosen to die. It is removed from the domain. However its tracer particle remains in place. The elements to the right of the dead element move to the left one element length, Δ, and a previously unmarked element becomes marked. (c) A marked element (hatched) dies and is removed. Its tracer particle remains where it is and causes the already marked element that was immediately to the right of the dead element to become doubly marked as it moves into the vacant space. There is no limit to how many tracer particles an element can accrue.

Deriving the continuum model

By changing the rate at which domain elements grow or die we can incorporate a variety of different types of domain growth/shrinkage. For each of these different types of tissue re-arrangement, using the first two infinitesimal moments (specifically the infinitesimal mean, &#956, and the infinitesimal variance, &#963²) of the domain growth process we can derive a continuum representation of the density of the tracer particles, C(x,t), on the domain:

These infinitesimal moments can be generated by considering moment generating functions of the corresponding birth processes.

Our generalised method allows for the derivation of the corresponding continuum model for a range of growth rates in the individual-based model: (i) Exponential growth, used to model elongation of the developing intestinal tract of the quail embryo, growth of sections of the embryos of the alligator Alligator mississippiensis, the initiation and positioning of teeth primordia in the same alligator species and the early stages of unconstrained cancerous tumour growth); (ii) Linear growth, used to model the early development of some fish, seeds and body sections of reptile embryos; (iii) Generalised logistic growth, used to model distance from the dorsal neural tube midline to the distal tip of the lateral mesoderm in chick embryos (a relevant cell migratory pathway) and the increase in mass of reptile and bird embryos; (iv) Gompertzian growth, used to model organ growth, tumour growth and alligator teeth patterning. Comparisons of the individual-based models and their continuum counterparts for three different growth rates are given in Figure3.

(a)

(b)

(c)

Figure 3: A comparison, at different times, of the expected occupancy of tracer particles on (a) an exponentially growing domain (b) a linearly growing domain and (c) a domain growing in according to generalised logistic growth. The red curves represent the solution of the Fokker-Planck equation and the (noisy) black curve represents the expected density of tracer particles averaged over 10,000 realisations of the individual based model. In all three cases the initial number of domain elements is 60, each of length Δ= ½, with tracer particles initially between 15 ≤ x ≤ 20. The curves are plotted at t = 15, 30, 45, 60.

Domain Shrinkage

The modelling of domain shrinkage is important for two reasons: (i) the explicit representation of domain shrinkage is often necessary for a range of application areas including wound healing, for example, (ii) the incorporation of element death is important in situations where domain elements may proliferate and die even if the net growth rate is positive. The second point is more subtle: it might be argued that domain growth in which element death is possible but the growth rate, b(t), outweighs the death rate, d(t), can be modelled using a purely growing domain with a reduced positive growth rate, λ(t) = b(t) − d(t). However, this argument is incorrect since, although the mean growth rate may be estimated correctly, the second and higher order moments of the process will be incorrect (c.f. Figure 3 (a) and Figure 4 (a). Both model exponential domain growth with the same net rate, but Figure 3 (a) shows the results from a purely growing domain where as domain elements of the domain used to generate Figure 4 (a) were capable of death as well as growth). In particular, one stark difference is that the domain in which death is incorporated explicitly will shrink to zero size with a non-zero probability, whereas there is no possibility of this happening in the purely growing domain with reduced net growth rate.

In order to illustrate the importance of domain shrinkage we incorporate elemental death into the model of domain growth and also consider a pure domain shrinkage model (see Figure 4). The infinitesimal moments required to populate the Fokker-Planck equation can be found by generalising the moment generating function approach to birth-death processes.

(a)

(b)

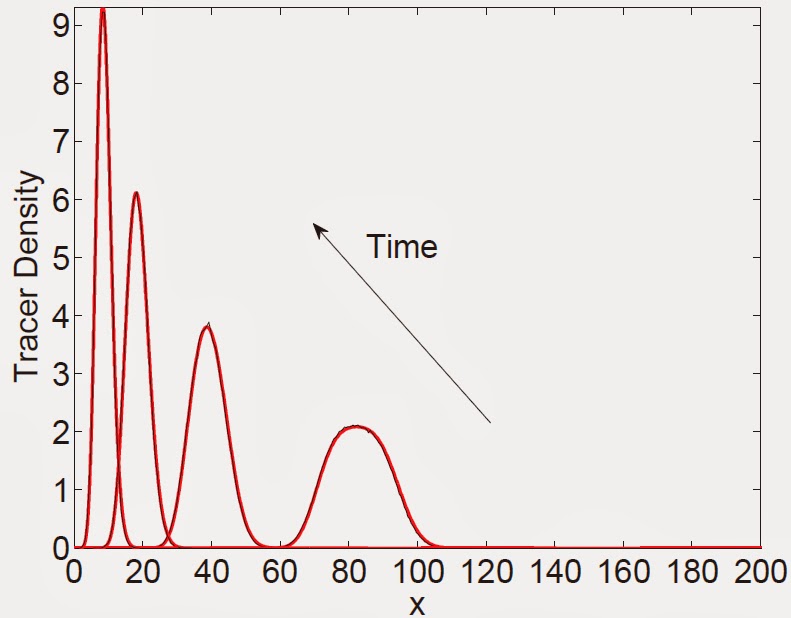
Figure 4: A comparison, at different times, of the expected occupancy of tracer particles on (a) a domain growing  exponentially with constant birth and death rates, b > d (b) an exponentially shrinking domain with  constant death rate, d. Figure descriptions and initial conditions for (a)  are as in Fig. 3. For (b) the initial number of domain elements is 600, each of length Δ= ½, with tracer particles initially between 150 ≤ x ≤ 200. Note that for (b), the time arrow is in the opposite direction.

Conclusions

Our generalised method allows the analytical derivation of the associated drift and diffusion coefficients for any time-dependent growth rate in the individual-based model. In addition, we have incorporated the possibility of elemental death into the individual-based model and derived the coefficients of the corresponding PDE for these general time-dependent birth and death rates. This approach highlights that a process in which both elemental birth and death occur cannot simply be approximated by a birth-only process with the reduced net growth rate since, although the drift coefficient may be correct, the diffusion coefficient will not be. Clearly, in situations in which the net birth rate is negative a simple birth process will not suffice.

For representative examples of our pure-birth, birth-death and pure-death processes we have carried out numerical simulations which contrast the expected tracer density in the individual-level model with the solution of the continuous PDE model and we see good agreement in each case.

As yet we have considered only the relatively straight-forward case of uniformly growing domains in which each element is selected to proliferate or die with equal probability. It is not immediately evident what effect, allowing anisotropic element proliferation will have on the corresponding drift and diffusion coefficients. A further challenge will lie in the adaptation of these methods to multivariate diffusion processes which will correspond to higher dimensional PDEs. Since tissue growth is an important factor in the transport of cells across the domain, and often does not occur uniaxially or uniformly, these extensions will constitute an important step forward in our ability to model cell migration effectively at both and individual and collective level.